Two types of projection
- Orthographic Projection(正交投影)
- Persperctive Projection(透视投影)
道理我都懂,所以鸽子为什么这么大?
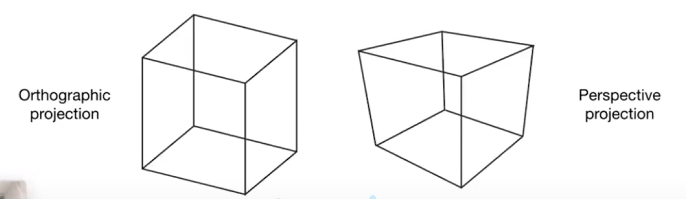
Orthographic Projection
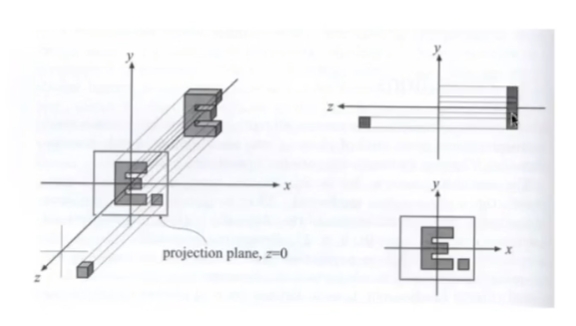
In general, we want to map a cuboid $[l,r] × [b,t] × [f,n]$ to the canonical cube $[-1,1]^{3}$ Here, the object will be stretched, but it will be stretched again during the subsequent viewport transformation.
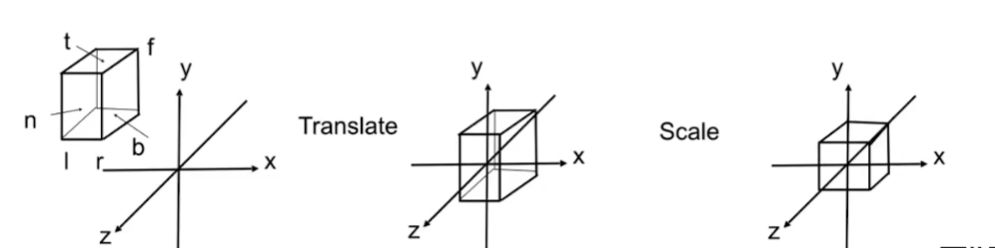
So, this matrix is this:
$M_{ortho} = S_{ortho} T_{ortho}$
Perspective Projection
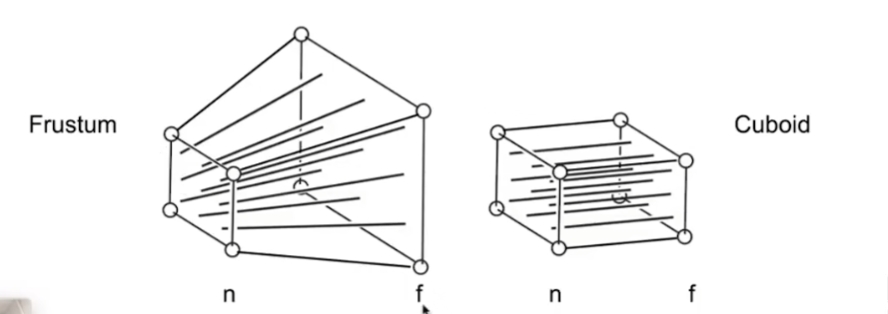
As shown in the figure, perspective projection on the x and y axes can be understood as a transformation of similar triangles.
Find the relationship between transformed points $(x,y,z)$ and the original points $(x_{0},y_{0},z_{0})$
$y = \frac{n}{z}y_{0}$
$x = \frac{n}{z}x_{0}$
in homogeneous coordinates
So, based on the results above we can now infer part of the matrix.
Any point on the near plane will not change
so the third row must be of the form $(0,0,A,B)$
$n^{2}$ has nothing to do with x and y, so we sure the first two number is $(0,0)$. Now let’s look at the center point of the far plane. Its ( x ) and ( y ) are both ( 0 ), and ( z = f ).
Solve for A and B
Finally, ervery entry in $M_{persp->ortho}$ is known! What is next? do orthographic projection to finish.
$M_{persp} = M_{ortho}M_{persp->ortho}$